上次介绍了顺序模型，但是在大多数情况下，我们基本都是以类的形式实现神经网络。

大多数情况下创建一个继承自 Pytorch 中的 nn.Module 的类，这样可以使用 Pytorch 提供的许多高级 API，而无需自己实现。

下面展示了一个可以从nn.Module创建的最简单的神经网络类的示例。基于 nn.Module的类的最低要求是覆盖__init__()方法和forward()方法。

在这个类中，定义了一个简单的线性网络，具有两个输入和一个输出，并使用 Sigmoid()函数作为网络的激活函数。

import torch from torch import nn  class LinearRegression(nn.Module):     def __init__(self):         #继承父类构造函数         super(LinearRegression, self).__init__()          #输入和输出的维度都是1         self.linear = nn.Linear(1, 1)      def forward(self, x):         out = self.linear(x)         return out

现在让我们测试一下模型。

# 创建LinearRegression（）的实例 model = LinearRegression() print(model)  # 输出如下 LinearRegression(   (linear): Linear(in_features=1, out_features=1, bias=True) )

现在让定义一个损失函数和优化函数。

model = LinearRegression()#实例化对象 num_epochs = 1000#迭代次数 learning_rate = 1e-2#学习率0.01 Loss = torch.nn.MSELoss()#损失函数 optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)#优化函数

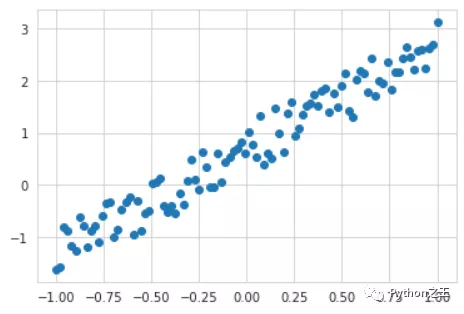
我们创建一个由方程产生的数据集，并通过函数制造噪音

import torch  from matplotlib import pyplot as plt from torch.autograd import Variable from torch import nn # 创建数据集  unsqueeze 相当于 x = Variable(torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)) y = Variable(x * 2 + 0.2 + torch.rand(x.size())) plt.scatter(x.data.numpy(),y.data.numpy()) plt.show()

关于torch.unsqueeze函数解读。

>>> x = torch.tensor([1, 2, 3, 4]) >>> torch.unsqueeze(x, 0) tensor([[ 1,  2,  3,  4]]) >>> torch.unsqueeze(x, 1) tensor([[ 1],         [ 2],         [ 3],         [ 4]])

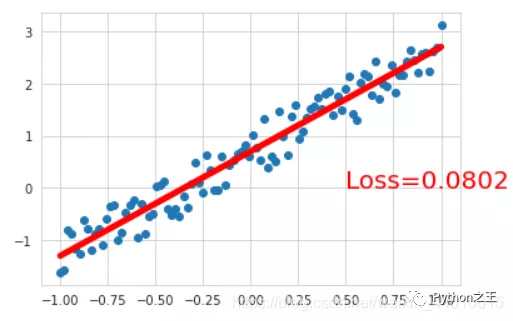
遍历每次epoch，计算出loss，反向传播计算梯度，不断的更新梯度，使用梯度下降进行优化。

for epoch in range(num_epochs):     # 预测     y_pred= model(x)     # 计算loss     loss = Loss(y_pred, y)     #清空上一步参数值     optimizer.zero_grad()     #反向传播     loss.backward()     #更新参数     optimizer.step()     if epoch % 200 == 0:         print(“[{}/{}] loss:{:.4f}”.format(epoch+1, num_epochs, loss))  plt.scatter(x.data.numpy(), y.data.numpy()) plt.plot(x.data.numpy(), y_pred.data.numpy(), r-,lw=5) plt.text(0.5, 0,Loss=%.4f % loss.data.item(), fontdict={size: 20, color:  red}) plt.show() ####结果如下#### [1/1000] loss:4.2052 [201/1000] loss:0.2690 [401/1000] loss:0.0925 [601/1000] loss:0.0810 [801/1000] loss:0.0802

[w, b] = model.parameters() print(w,b) # Parameter containing: tensor([[2.0036]], requires_grad=True) Parameter containing: tensor([0.7006], requires_grad=True)

这里的b=0.7，等于0.2 + torch.rand(x.size())，经过大量的训练torch.rand()一般约等于0.5。