本文经AI新媒体量子位（公众号ID:QbitAI）授权转载，转载请联系出处。

机器学习日常：不是在建模，就是在建模的路上。

而在建模过程中，又能听到炼丹爱好者时而念念有词“怎么又过拟合了？”，时而自我安慰“找到偏差和方差的平衡点是成功的诀窍”。

所以为了能让非专业者也能愉快地玩（zhuang）耍（bi），今天就来科普一下机器学习的几个常见概念。

泛化

如何判别一个每天都刷题的高中班级的成绩怎么样呢？

拉去考一场。

那怎么判断一个机器学习领域的新算法到底棒不棒呢？

去新数据里溜一圈。

这种对于训练集以外的数据也能进行良好的判别，或得到合适输出的能力，就称为机器学习模型的泛化（generalization）能力。

并且，说一个模型泛化能力弱，那也是有很多种弱法的。

过拟合与欠拟合

有些模型，直接死在提取数据特征这一步。

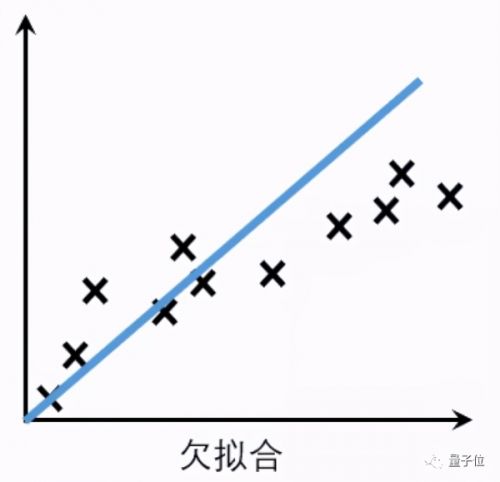
训练集上就没有完全拟合数据，实际样本中的表现同样误差很大。

类似一个高中生每天都拿着五三刷，但是始终找不到做题规律，模拟题做得拉跨，考试就更不用说。

这种在训练集和测试集（实际样本）中都表现不好的情况，就叫做欠拟合（Underfitting）。

这通常是因为模型复杂度低引起的（就是菜得很实在）。

而有些模型在训练时表现良好：

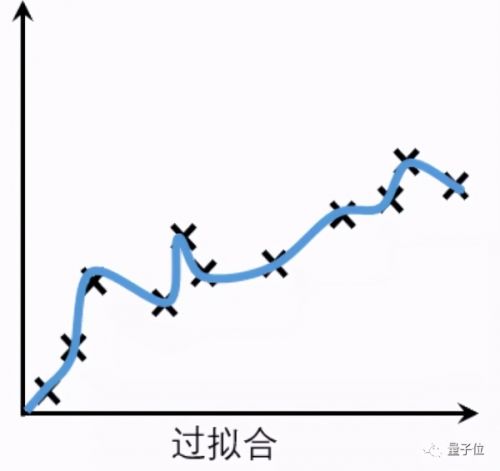
但一到实战就扑街。

这种在训练集上表现良好，但在测试集上表现很差的情况，就叫做过拟合（Overfitting）。

训练集质量不高就可能导致过拟合，比如样本不足，或者训练数据中的噪声（干扰数据）过多。

也有可能因为模型复杂度高于实际问题，只是死记硬背下了训练数据的信息，但完全无法推广到没见过的新数据上。

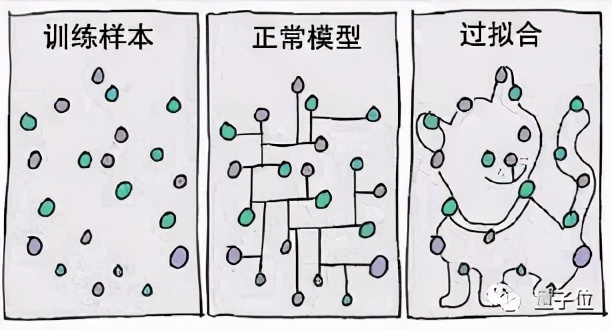
不管菜到底有几种方式，对于一个机器模型来说，总归是在实际应用里表现不好，发生了泛化误差（Generalization Error）。

而这种误差，可以再次细化为两个方面：

误差（Error） = 偏差（Bias） + 方差（Variance）

偏差与方差

在机器学习领域，偏差（bias）是指模型的预测值相对于真实结果的偏离程度。

△其中f(x)为预测函数，y为样本数据真实值

而方差（variance）与真实值没有关系，只描述通过模型得到的预测值之间的分布情况。

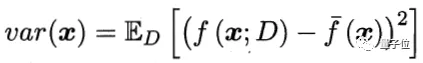
对于一个模型来说，偏差反映模型本身的精确度，而方差则衡量模型的稳定性。

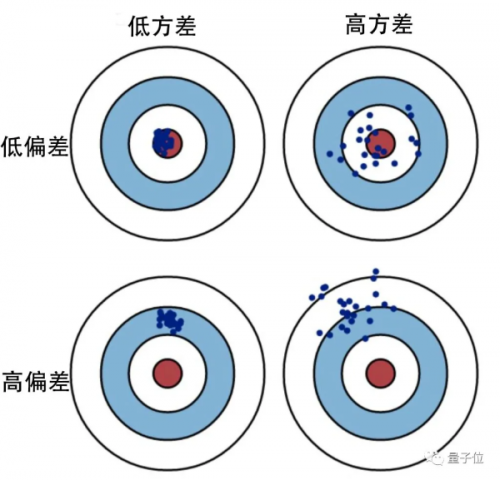
如果模型过于简单且参数很少，那么它可能具有高偏差和低方差的特征，也就会造成欠拟合。

而如果模型复杂而具有大量参数，那么它将具有高方差和低偏差的特征，造成过拟合。

看上去，一个好的机器模型就是要同时追求更低的偏差和方差。

但在实际应用中，偏差和方差往往不可兼得。

偏差与方差的权衡

先来看这两个模型：

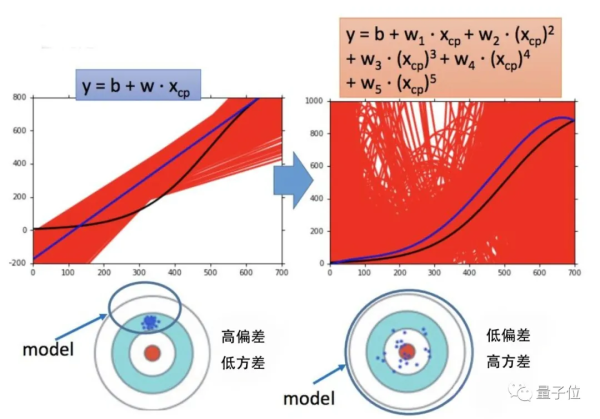
右边的模型明显比左边要复杂很多，也因此它的偏差更低，方差更高，与左边的模型相反。

这种偏差与方差之间的冲突就是偏差-方差窘境（Bias- Variance dilemma）：

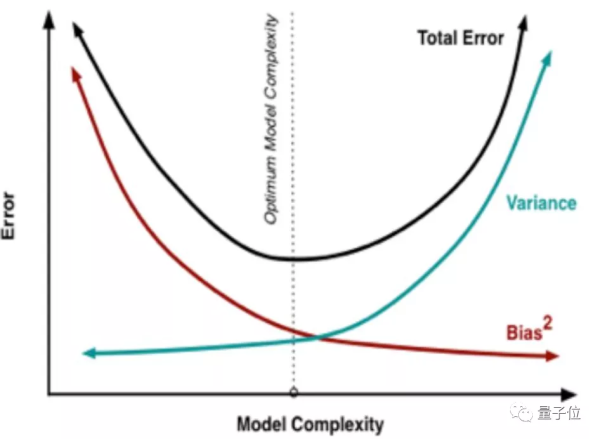
在改进算法时，要减少偏差就会增大方差，反之亦然。

因此，我们需要找到一个合适的平衡点，既不会因为高偏差而造成欠拟合，也不会因为高方差而造成过拟合。

这种偏差与方差之间的权衡（bias and variance trade-off），实际上也就是模型复杂度的权衡。

为什么要提出这些概念？

简单来说，为了让计算机也学会人类的概括能力。

比如，如果我们要通过某地房屋面积与房价之间的关系，进而帮助房屋售卖者选取更合适的售价，那么下面哪个函数最好呢？

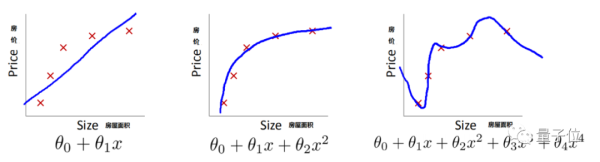
△红色为事先给定的样本数据

第一个明显欠拟合。都没有从给定的数据中找到一般规律，更不用说让函数去预测新房价面积可能对应的售价了。

第三个就是过拟合，函数参数过多，想要抓住所变化，反而导致模型的通用性下降，预测效果大打折扣。

而第二个函数基本拟合了样本数据，形成了一般规律，也保证了对新数据的预测能力。

能从海量数据中找到一般规律，这就是一个模型的泛化能力。

模型的泛化能力越高，通用性也就越强，这样能完成的任务范围也就越广。

但就算是ANN（人工神经网络）这样优秀的机器学习模型，目前也还是受限于偏差与方差的权衡。

算法工程师们提出了各种方法，如正则化（Regularization)、套袋法（Bagging）、贝叶斯法（Bayesian)，使模型能够更好地概括旧数据，预测新数据。

并期望着最终能构建一个机器学习模型，使其能力无限逼近目前最强的通用模型——人类大脑。